Essa é a segunda parte da nossa série entendendo a matemática, a qual nós começamos com uma introdução à lógica matemática. A ideia dessa série é te apresentar tópicos da matemática importantes para você compreender sua verdadeira estrutura, ao invés de ficar decorando fórmulas e fazendo milhares de contas no papel. Fazer isso não gera nenhum dos benefícios citados no post a importância da matemática para a programação, pelo contrário, só vai te frustrar e fazer com que desista de estudar.
A definição é uma sentença que evidencia propriedades e características inerentes ao objeto de tal modo que o distinguia dos demais. Aqui estão alguns exemplos de definições apresentadas em teoria dos conjuntos e geometria plana.
Definição 1 (D1): Dados dois conjuntos A e B, chamamos união de A e B o conjunto formado pelos elementos que pertencem a A ou a B.
A = {1, 3}
B = {2, 4}
A ∪ B = {1, 2, 3, 4} (lê-se A união B ou A reunião B ou mesmo [re]união de A e B)Definição 2 (D2): Dados dois pontos distintos A e B, a união do conjunto desses pontos com o conjunto dos pontos que estão entre A e B é um segmento de reta.

Definição 3 (D3): Dados 3 pontos, A, B e C, que não pertencem a mesma reta, chamamos triângulo ABCΔ a união (D1) dos segmentos de reta (D2) AB, AC e BC.
Antes de continuar o assunto, irei fazer algumas observações: Para definirmos um objeto A através de um objeto B, precisamos ter definido o objeto B previamente. O exemplo acima destaca isso, pois definimos união de conjuntos e segmento de reta para depois definirmos triângulo. O único problema é que usar uma palavra pra definir outra pode acabar gerando um ciclo onde usamos A para definir B e B para definir A ou então teríamos de definir tudo sem parar.
As noções primitivas ou noções comuns são conceitos que adotamos sem uma definição, pois deles temos entendimento intuitivo via observação e experimento. Note que nos exemplos anteriores, algumas palavras foram destacadas em negrito e itálico. Todas essas são noções comuns, por isso não foi necessário defini-las antes usá-las.
A definição de um ente matemático pode gerar o que chamamos de consequência da definição, que é, literalmente, algo que decorre da definição. Pode parecer besteira, mas muitas vezes conseguimos resolver problemas através das consequências de uma definição. Vamos ver um exemplo.
Definição 4 (D4): Seja a um número real maior ou igual a 0. Chamamos raiz quadrada de a o número b se, e somente se, b elevado a 2 é igual a a. Em símbolos:

Decorre dessa definição que o quadrado da raiz de a é igual ao próprio a
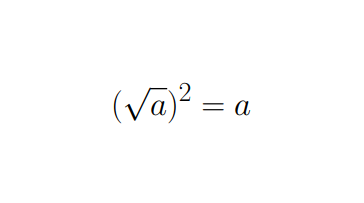
Isso pode ser útil, por exemplo, na resolução de uma equação cuja incógnita esteja “dentro” de uma raiz
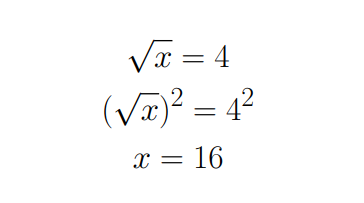
Para resolver essa equação, nós elevamos os dois membros da equação ao quadrado e “removemos” a raiz do x. Só conseguimos fazer isso graças à consequência da definição que nos diz que o quadrado da raiz de x é igual ao próprio x. Mas, e por que o 4 também foi elevado ao quadrado? Bom, isso é algo que pode ser explicado em outro artigo, por enquanto encerramos aqui.
Concluímos a segunda parte dessa série. Espero que tenham conseguido entender os tópicos abordados e, caso tenham ficado com alguma dúvida, podem deixar nos comentários. Críticas e sugestões também são bem-vindas.