Introdução à lógica

No artigo anterior, vimos um pouco sobre as aplicações da matemática na área de programação e destacamos que é de extrema importância estudá-la do jeito certo. É importante salientar que “estudar do jeito certo” significa compreender verdadeiramente como a matemática funciona e não ficar decorando fórmulas (isso não agrega em nada!!). Por exemplo, na matemática muitas fórmulas são deduzidas logicamente por um processo de pensamento. Ao decorar as fórmulas, você está apenas armazenando informação, no entanto, se você se esforçar para entender o processo até o resultado, se tornará uma pessoa mais criativa. Dito isso, esse artigo visa te apresentar a matemática de maneira menos superficial e te dar um norte de como você pode, de fato, estudar do jeito certo.

Noções de lógica

Para compreender bem conceitos como definições, axiomas e teoremas é necessário, antes de tudo, começar pela base. Similar a programação, a base da matemática é a lógica.

Sentença

Uma sentença ou proposição é uma oração de sentido completo e de caráter afirmativo. Em outras palavras: é uma frase afirmativa. Aqui vão alguns exemplos de proposições matemáticas.

5 > 2 // lê-se cinco é maior que dois
2 = 1 // lê-se dois é igual a um

Outro fato importante sobre as sentenças é que elas satisfazem a dois princípios: o da não contradição e o do terceiro excluído. Isso quer dizer que uma sentença só pode ser verdadeira ou falsa, mas não as duas simultaneamente (pois seria uma contradição) e não há uma terceira opção. Além disso, sentenças possuem sujeito, verbo e predicado. Aqui estão exemplos de não sentenças.

2 x 3 // não é uma oração afirmativa
3 - 3 // não é uma oração afirmativa
x > 2 // não é uma sentença

Mas como assim?! O terceiro exemplo contém tudo que foi dito: é uma oração afirmativa com sujeito, verbo e predicado. Por que não é uma sentença? No caso desse exemplo, se trata de um tipo particular de sentença chamado de sentença aberta. Mas como não podemos deduzir seu valor lógico por não conhecermos o valor de x, então também não podemos chamar apenas de sentença. Como curiosidade: uma maneira de “fechar” essa sentença é através dos quantificadores universal e existencial da matemática.

Conectivos

As sentenças apresentadas anteriormente são ditas simples, mas existem as sentenças compostas, as quais apresentam mais de uma proposição ligadas por um conectivo. Alguns conectivos são os de conjunção, disjunção e o condicional.

Conjunção e Disjunção

Esses conectivos são conhecidos por qualquer programador, pois se tratam do e e ou lógicos. A regra para esses conectivos é bem simples: dadas duas proposições p e q, a conjunção entre p e q é verdadeira apenas se p e q forem verdadeiras. Já a disjunção vai ser verdadeira se, pelo menos, uma das proposições, p ou q, for verdadeira.

Condicional

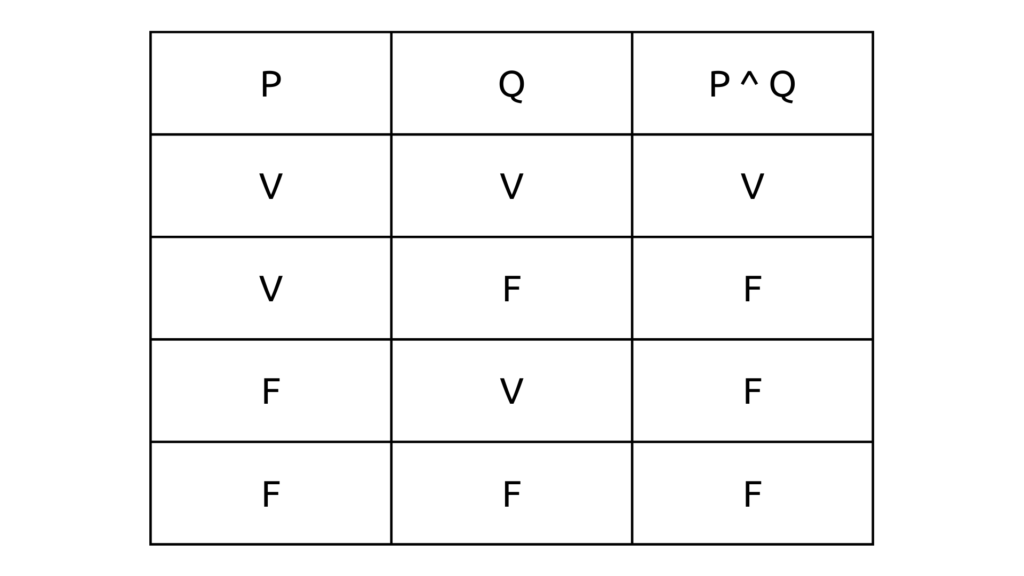
Um conectivo desconhecido por muitos programadores, mas essencial na matemática é o se, então. A regra para ele também é bastante simples: dadas duas proposições p e q, a proposição composta se p, então q é falsa apenas quando p for verdadeira e q for falsa. A princípio parece não fazer sentido, mas a explicação para isso é que não é possível deduzir uma sentença q falsa a partir de uma sentença p verdadeira. Guarde isso, será importante para entender demonstrações.

Implicativa

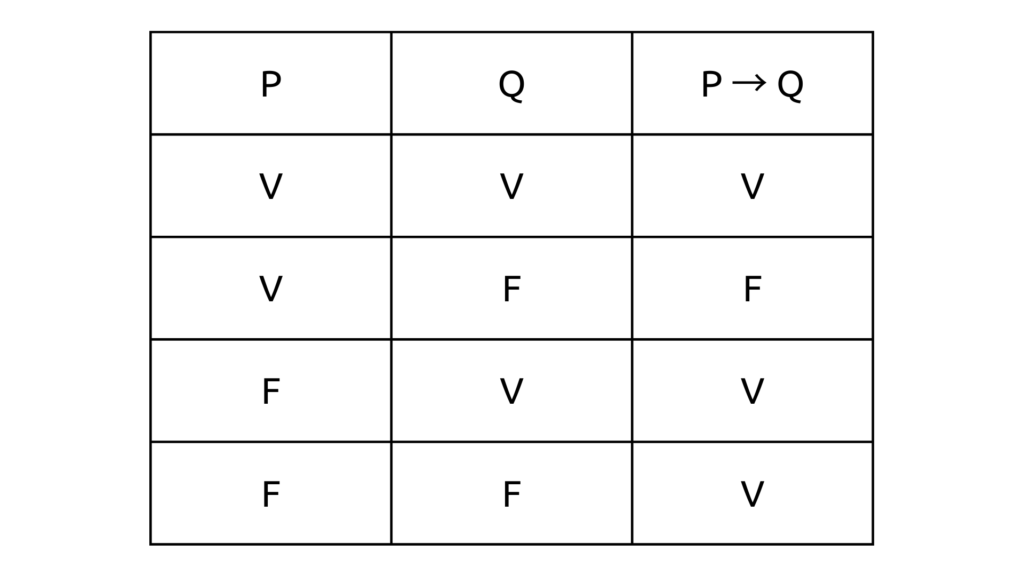
Uma sentença implicativa é uma sentença composta ligada pelo conectivo implica. A lógica é equivalente ao se, então. Dadas duas proposições p e q, dizemos que p implica q apenas se p e q não forem respectivamente verdadeira e falsa. Sua tabela verdade é exatamente igual a do se, então, por isso dizemos que as sentenças se p, então q e p implica q são sentenças equivalentes.

Negação

A negação também é muito comum na vida de programador. Negar uma proposição significa inverter seu valor lógico. Se p é uma proposição verdadeira, a proposição ~p (lê-se negação de p) é falsa e ~~p (lê-se negação da negação de p) é verdadeira.

9 ≥ 2 // verdadeiro
~(9 ≥ 2) // falso

Se fôssemos escrever a negação do exemplo acima, teriamos essa proposição: 9 < 2 (que de fato é falsa). A justificativa é que algo que não é maior ou igual, é menor.

Símbolos da programação

Apesar da lógica ser a mesma, os conectivos apresentados têm símbolos diferentes dos que costumamos usar. Isso acontece porque a matemática tem seus próprios símbolos para representar os conectivos. Abaixo você pode ver os exemplos anteriores adaptados em uma linguagem de programação.

5 > 2 // true
2 == 1 // false
!(9 >= 2) // false
!!(9 >= 2) || 1 != 1 // true
!(2 > 2) && 3 <= 3 // true

Conclusão

Todos esses tópicos abordados compõem a matéria de lógica matemática, mas a própria lógica de programação usa alguns conceitos. Na verdade, como programadores, lidamos com proposições e conectivos toda hora, apenas chamamos por outros nomes: as proposições são operações relacionais como igualdade, identidade e diferença, os conectivos são os operadores lógicos e as sentenças compostas são a combinação de operações relacionais e lógicas. Esse artigo será dividido em mais de uma parte para não ficar muito cansativo de ler. Caso tenha ficado alguma dúvida, deixe na seção de comentários.